In the fast-paced world of financial markets, the ability to systematically evaluate the performance of trading strategies is critical. Backtesting provides a data-driven approach to assess the historical performance of trading algorithms, enabling us to research and refine our strategies. Furthermore, we can evaluate algorithms on synthetic data to assess their robustness to stress scenarios and response to market risks. The computational performance of backtesting frameworks is often a limiting factor on the optimisation fidelity or the precision of risk metrics we can evaluate. Here we present a framework for accelerating the construction of historical price data. The presented method reduces the relevant calculations for candles by factors of up to $1.2\times 10^5$ as shown in the below table. \[ \begin{array}{l|l|l|l} \text{Request}& \text{Operation count} & \text{Reduced operation count} & \text{improvement factor} \\\hline 100\times 1\text{Min} & 1.2\times 10^5 & \leq 1200 & \geq 100\\ 100\times 1\text{Hour} & 7.2\times 10^6 & \leq 1320 & \geq 5400\\ 100\times 1\text{Day} & 1.7\times 10^8 & \leq 1370 & \geq 1.2 \times 10^5 \end{array} \]

Many trading algorithms execute once an asset price or an indicator breaches a threshold value. The precise development of price action, which is lost in the usual OHLC candle representation, can thus have a significant impact on the backtest precision. We therefore often have no choice, but to evaluate strategies with tick-level data precision incurring considerable computational costs.

When working on tick-level data we have both the bid and ask prices of an asset each time the price changes. This differs from OHLC candles, which only contain the open-, high-, low-, and close-prices of an asset for a given timeframe, such as 1Min, 1Hour, or 1Day. Such candle-level data is often used to calculate indicators on which we may base trading strategies. 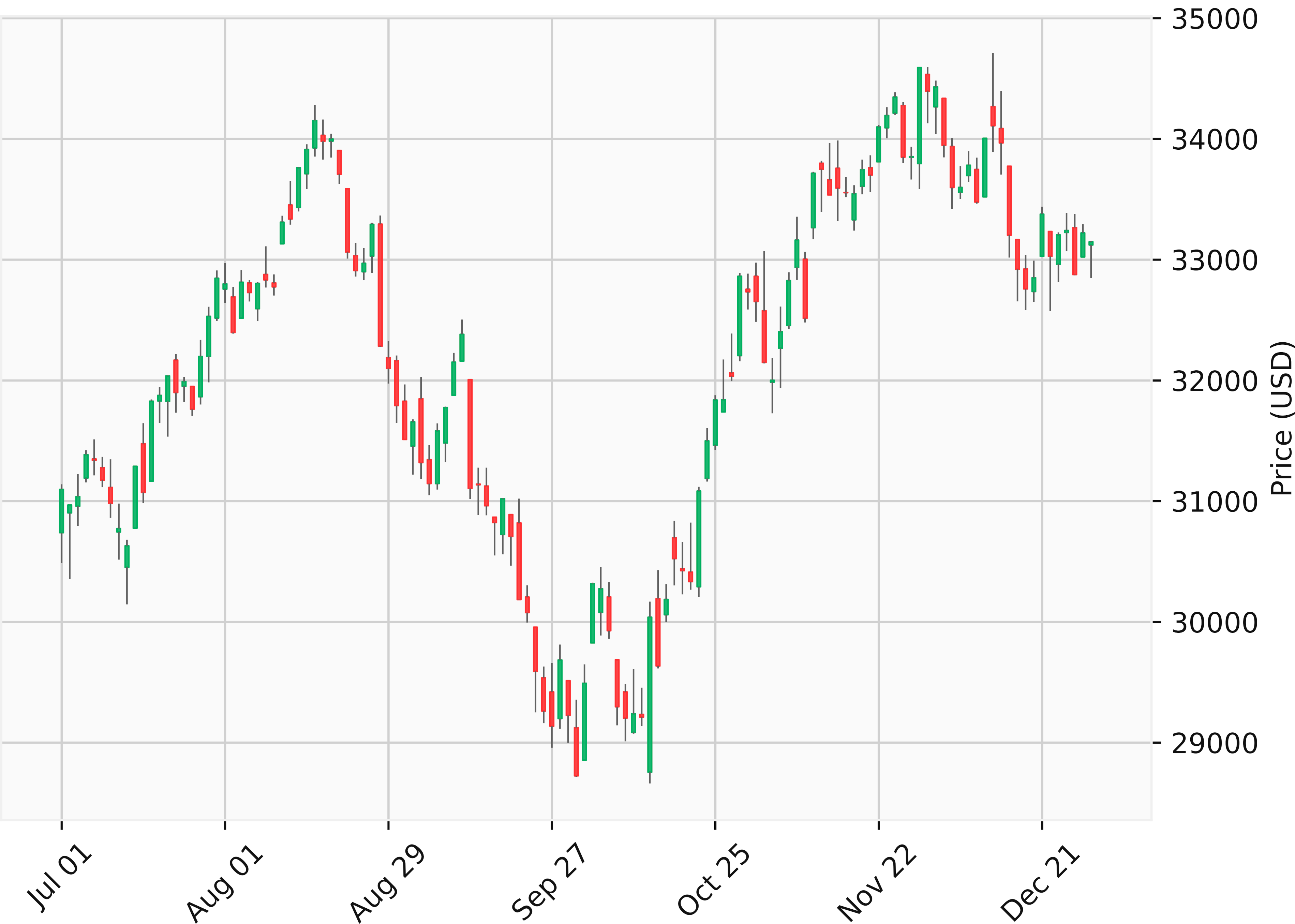We can reconstruct candle-level data from tick-level data by aggregating the relevant ticks, which fall within a candles time bounds and evaluating the first, last, maximal, and minimal prices. The below images visualises such candle structures by showing daily price candles on DowJones (US30) prices from the second half of 2022.

While the calculations for candle reconstruction are simple, they quickly become computationally costly when performed at scale. Consider a liquid and continuously traded asset like BTC, and assume that on average we observe 10 ticks each second. This implies we require 864,000 ticks to calculate the daily high and low prices, indicating the high computation cost when done at scale. During a backtest, we generally keep a simulated time point, which we increase progressively while executing the strategy logic. This means that the most recent candle needs to be updated at each time step, incurring significant computational cost.

Algorithmic design:

One way to reduce the computational cost is to exploit the forward-only structure of backtest data. However, this prevents us from effectively running multiple simulation in parallel on the same set of tick-data. We are looking for a data-structure that allows us to efficiently query candle. For these queries the end times will generally not align with candle end points, in such cases we want the last returned candle to be composed of ticks which are known up to end query end time. The tick engine we present here achieves this by exploiting the hierarchical structure, which is inherent to trading candles.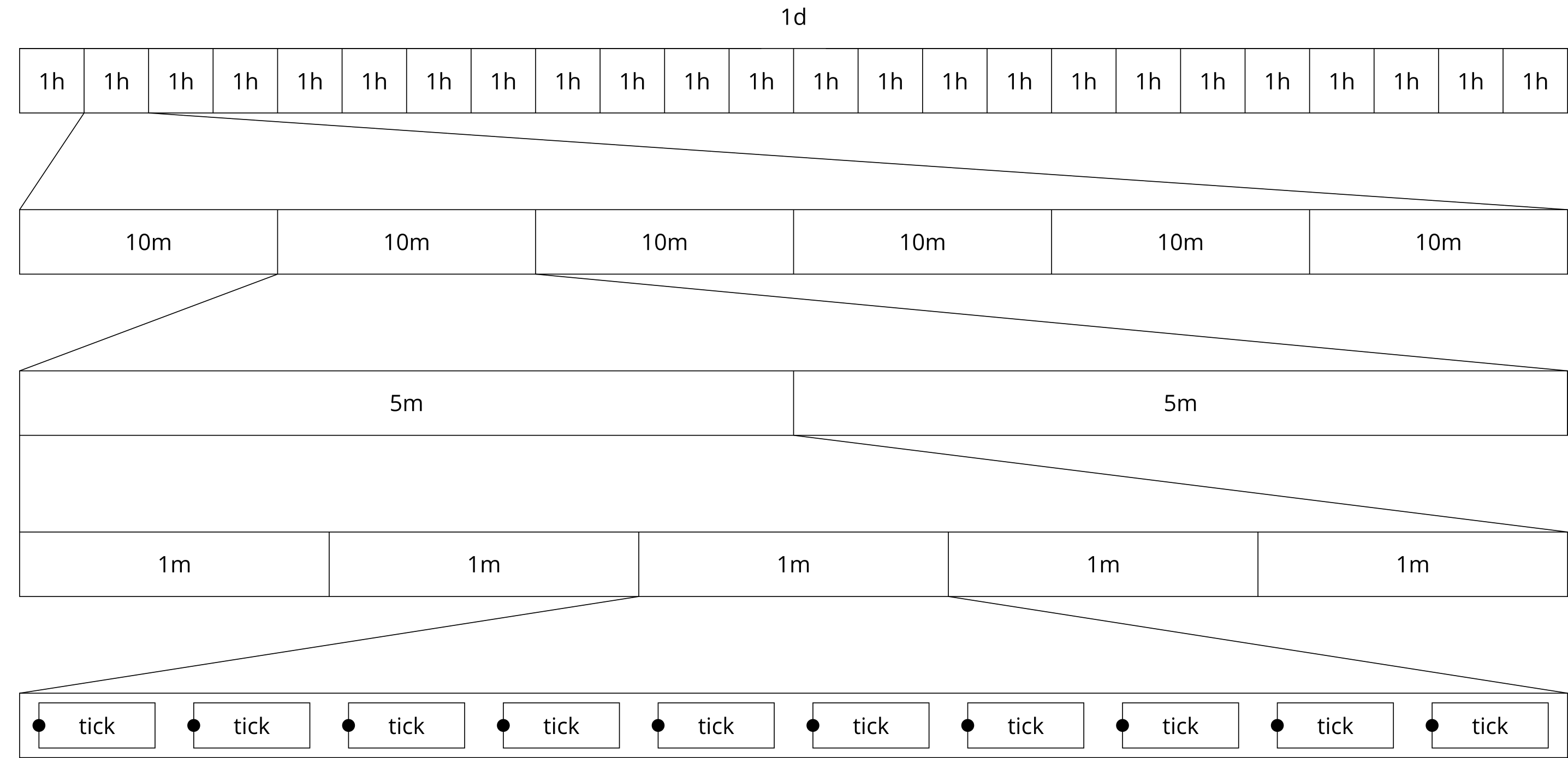
By exploiting this hierarchical time structure effectively we can request an arbitrary number of candles while only having to consider tick-level price information from the most recent 1Min, achieving considerable performance benefits.

Rust implementation and performance aspects:

The implementation of this project can be found here. The core of this project is implemented in Rust to realise performance benefits over a Python implementation. As the above discussion heavily considers the performance aspects of backtesting environments it is natural to choose a language, such as Rust, that allows for performance optimised code. Due to Rust's rich type system and effective memory management, handled by the borrow checker, we can realise further performance benefits with a zero-copy oriented implementation. When candle requests do not need to modify the underlying data, we can use rusts borrow rules to only provide a read-only data view, which reduces the computational cost further by reducing memory allocation and copy cost. The implemented package exposes the required functionality to Python using PyO3, allowing us to use this optimised tick engine in our Python projects.